Finding Sierpiński in the Oddest Places
This is a tale of finding fractals in an unexpected place and why the appearance makes sense in hindsight.
I was looking for patterns in valid board game configurations, specifically the middle contesting row in the Game of Ur. In the game, there are eight slots either of the two players may occupy, but a slot may only be occupied by at most one player. I represented the available slots as two bit strings, with each bit representing a single slot. A valid placement is one where the two corresponding bits are both false or only one is true, but never both are true. Formally, this is equivalent to the bitwise formula \(\neg (p \land q)\) or \(p \uparrow q\).
Plotting the p and q bitstrings as axes within a matrix, I saw:
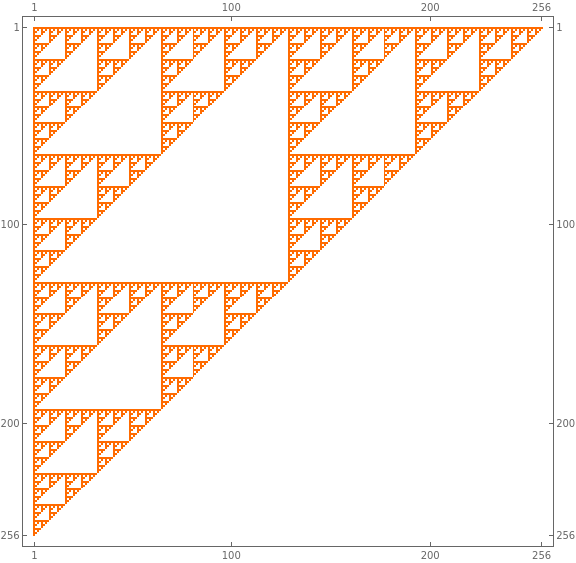
I recognized this set of repeated triangles as a Sierpiński Triangle (or Gasket). Described by Wacław Franciszek Sierpiński in 1915 (mathematically; there may have been artistic representations in the 13th century by the Cosmati1), the Gasket is an iterative structure with infinite scaling. The Triangle is considered a fractal (and one of the first discussed in any primer), but the discovery predates the field of fractal geometry. A typical way to describe the construction2 is to inscribe a triangle with coordinates (0,0), (0,1), and (1,0). Then, inscribe three triangles via the transformations:
- \((x,y) \rightarrow (\frac{1}{2}x, \frac{1}{2}y) \)
- \((x,y) \rightarrow (\frac{1}{2}x + \frac{1}{2}, \frac{1}{2}y) \)
- \((x,y) \rightarrow (\frac{1}{2}x, \frac{1}{2}y + \frac{1}{2}) \)
Animating this construction (note that this figure has been rotated versus the matrix orientation):
Of course, the Triangle’s representation can also be rotated and projected without impacting the structure. Equilateral constructions are very popular.
There are many ways to construct the Triangle, including many that aren’t graphical. The Triangle is registered as OEIS A001317 Sierpiński’s triangle (Pascal’s triangle mod 2) converted to decimal. The catalog entry contains 16 formulas and 17 links. Due to the link to Pascal’s Triangle, which has a tremendous number of constructions, this is a small subset of the known set.
Looking through the catalog, I tried to find one that corresponded to how I was generating the Triangle but didn’t find one. The exclusive-or method — \(a_{n+1} = a_n \otimes 2*a_n\) — seemed like a good candidate, but I did not find an an algebraic equivalence.
Since my formulation wasn’t generating integers but rather a binary matrix, I found a different formulation that was defined for binary matrices:
$$a_{i=1,j=*}=1$$
$$a_{i=*,j=1}=1$$
$$a_{i,j} = a_{i-1,j} \otimes a_{i,j-1}$$
This formulation can be easier to see in smaller matrices:

I was still having difficulty finding an equivalence between this formula and mine, although the above seemed closer. In particular, I started thinking of the representations of binary numbers and how my ordering incorporated binary operations. Thinking that I might have discovered a novel representation, I expanded my research and found that, yes, someone had discussed this construction before (and they didn’t even treat it as novel). Alas.
Fractal Images of Formal Systems3 explores the intersection of formal systems (e.g. propositional calculus) and fractals via visualizations. (Academic works tend to be what they say on the tin.) In one of the examples, the authors explore computing NAND (not and; often depicted via the Sheffer stroke \(\uparrow\)) of two sentences of propositions. They found that ordering these sentences into ascending order and plotting the results yielded a Sierpinski Triangle. This approach is analogous to my application of NAND’ing two binary strings.
So, why is the Triangle generated by the NAND of two bitstrings, projected onto a two-dimensional matrix? Drawing upon the discussion in Fractal Images:
First, we can consider one of the classic constructions (similar to before): For any given triangle, the interior points can be divided into two classes. The first class of points are ones where, if we measure the distance from them to the closest vertex of the surrounding triangle, a doubling of that distance would be outside the triangle. The second class of points are the ones where the doubling of the distance would be inside the triangle. The first class will form an empty inverted triangle in the center. Of the points in the second class, we can repeat the process by separating points that would be outside the triangle by twice doubling the distance versus ones that would be inside. A Sierpiński Triangle is formed via the infinite repetition of this process.
How can we map the above construction of the Triangle into our NAND matrix world? Consider the NAND logic inscribed on a unit square, where the true values are connected to form a triangle:
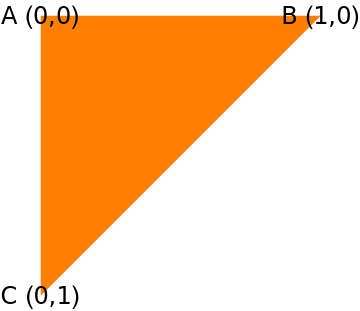
If we implement the doubling logic within this unit square, the logic acts as:
| Closest Vertex | Translation |
|---|---|
| A (Origin) | \( (x,y) \rightarrow (2x, 2y) \) |
| B (1,0) | \( (x,y) \rightarrow (1 - 2(1-x), 2y) \rightarrow (2x - 1, 2y) \) |
| C (0,1) | \( (x,y) \rightarrow (2x, 1 - 2(1-y)) \rightarrow (2x, 2y - 1) \) |
(It may be helpful to think of an inward pointing vector from the vertex.)
What does doubling mean in terms of numbers encoded as binary strings? Multiplying a binary number by 2 is equivalent to a left shift (and halving is equivalent to a right shift). Subtracting a one will invert the lowest bit (among other potential changes).
Shifts either insert a zero at the lowest bit or remove the lowest bit from the string. A pair of zeros will not change the result of a NAND computation, so if two strings are valid, we can left shift them infinitely with no change. Similarly, if two strings are valid under NAND, stripping the lowest bits will not change the result of the computation.
Subtracting the one will eliminate any one-bits on the lowest bit. If the lowest bit is not set, this leads to an arithmetic subtraction that may invert a number of bits depending on the original string (borrowing). How does borrowing avoid violating the NAND rules? For the two original strings, there are three possibilities for the lowest bits: x=0 y=0, x=0 y=1, and x=1 y=0. (The case of x=1 y=1 would be invalid per NAND.) For the second and third case, the subtraction will borrow from a placement of 1 leading to a valid string. For the first case, rule A does not require borrowing. Thus, the recursive nature of the construction remains valid under the rules of NAND and the Triangle is approximated by NANDing binary numbers.
-
Brunori P., Magrone P., Lalli L.T. (2019) Imperial Porphiry and Golden Leaf: Sierpinski Triangle in a Medieval Roman Cloister. In: Cocchiarella L. (eds) ICGG 2018 - Proceedings of the 18th International Conference on Geometry and Graphics. ICGG 2018. Advances in Intelligent Systems and Computing, vol 809. Springer, Cham. Author PDF ↩︎
-
Falconer, Kenneth. Fractals: A very short introduction. OUP Oxford, 2013. ↩︎
-
Denis, Paul St, and Patrick Grim. “Fractal images of formal systems.” Journal of philosophical logic 26.2 (1997): 181-222. PDF HTML ↩︎