Surviving the Blizzard: An Application of Markov Chains
In the Call of Cthulhu adventure “Chateau of Blood”, the characters are faced between spending the day trapped in an ominous chateau where they will likely be attacked by monsters or attempting to navigate a treacherous mountain trail as a ferocious blizzard blows. Inspired by Hammer films, the characters are encouraged to stay inside the chateau, find clues, and face the monsters rather than go out into almost certain doom. However, as this is a Hammer film, few are expected to survive the supernatural horrors. What are the character’s chance in the storm? We’ll use Markov chains and a short Rust program to work out the odds.
Formulating the Approach
If the characters decide to leave the (relative) safety of the chateau and attempt to travel to Karlensburg (the closest town) while the blizzard rages, the adventure describes the mechanics thusly:
In these conditions, Karlensburg is a ten-hour walk and a seven-hour horseback ride. Travel by coach is impossible. Roll D100 each hour. Initial CON x5 roll or lose 1 hit point the first hour; in the second hour, the lose for a missed CON roll is 2 hit points, in the third hour 3 hit points, and so on. Further, each time a CON roll is failed, thereafter lower the multiplier by one: thus one failed CON roll lowers the multiplier to x4. [1]
At this point in the adventure, characters may have suffered damage. They may or may not have access to horses, depending on earlier events.
What are the key aspects of this mechanic?
- There are four numbers that matter: the character’s CON score (which is constant), the number of hours spent traveling, the number of failed rolls, and the amount of damage accumulated.
- Trips conclude when the number of hours match the mode of travel. A successful trip is one where damage accumulated is less than the character’s hit points.
- Each roll of the dice equals an hour of travel.
- The die roll is the only mechanism that leads to a change in state.
This is a stochastic process; a random variable (the die roll) solely maps the event (the success or failure determination) to different numbers (the state) at different times. Since the next state can be computed given only the current state, this process is a first-order Markov process. Furthermore, since time moves discretely and state is discrete, this is a Discrete-time Markov Chain [2].
This is useful because various facts about discrete-time Markov chains can be computed efficiently, including the probability of various states.
We can express the Markov property as:
$$ P[X_k=j | X_{k-1} = i] = p_{ij} $$
That is, the probability of state X at time k, given the state at time k-1, is equal to the probability stored in the matrix p at index i, j.
The matrix p must satisfy the conditions [3]:
- \(0 \le p_{ij} \le 1\)
- \(\underset{j}{\sum} p_{ij} = 1, i=1, 2, \mathellipsis, n,\) which follows from the fact that the states are mutually exclusive and collectively exhaustive
If we want to know the probability of being in a state m after n transitions given an initial state I (a column vector), we can compute it using p with:
$$ m = p^n * I $$
where m will be a column vector containing the probability of each state.
Implementing a Solution
Since we have decided to use Markov chains, we need a matrix implementation which supports products. This is not a hard reach. Furthermore, because the transition matrix will only contain a maximum of \(2^{hours}\) entries, but be of size \(2^{hours} \times 2^{hours}\), we would prefer using sparse matrices to conserve memory. After first considering running the calculation within the browser via WASM, I decided that the “universe of solutions” was small enough I should instead just write a file with all solutions.
A 7x7 subset of the transition matrix p:
$$ \begin{pmatrix} 0 & 0 & 0 & 0 & 0 & 0 \\ 0.6 & 0 & 0 & 0 & 0 & 0 \\ 0.4 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0.6 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0.48 & 0 & 0 & 0 \\ 0 & 0.4 & 0 & 0 & 0 & 0 \end{pmatrix} $$
I chose Rust for “reasons” and, browsing lib.rs, chose sprs, a “sparse linear algebra library”. Alternatively, I could have used Mathematica (which I did use for validation and visualization), Python and scipy, Scala, or JavaScript and math.js. If I was feeling very industrious, I could have used either of the sparse libraries that come with Netlib sparse/sparse-blas. The requirements for this implementation are very trivial.
The main function loops through all possible CON, hit point, and travel mode possibilities, solving each and outputting the results to stdout formatted as a CSV file:
fn main() {
println!("hours,CON,hp,alive,dead,alive + dead");
for con in 3..=18 {
for hp in 1..=20 {
for hours in vec![7, 10] {
let character = Character { con, hp };
let (states, mat) = build_transition_matrix(&character, hours);
let (alive, dead) = survival(hours, character, states, mat);
println!("{},{},{},{},{},{}", hours, con, hp, alive, dead, alive + dead);
}
}
}
}
When we build the transition matrix, we need to decide how we are going to an index within the matrix to a state. Within the program, TravelState is the “friendly” way to track a character’s progress. I originally planned to map the states using a bitmap approach — use 4 bits for hours, 3 bits for fails, and 5 bits for damage, all packed within a unsigned 16 bit integer. Although the representation can be more clever and save a few bits, we still ended up with unrepresentable states. The transition matrix must have at least one value in every column (each column must sum to 1), so we either need to manually insert dummy values into non-representable states or map indices in a different way.
#[derive(Copy, Clone, PartialEq, Eq, PartialOrd, Ord, Debug)]
struct TravelState {
/// hours spent within the blizzard [0, 7 or 10]
hours: u8,
/// total number of times PC has failed the CON check [0, 5]
fails: u8,
/// accumulated hit point damage from the blizzard [0, 18] or hit points of character
damage: u8,
}
impl TravelState {
/// Initial state for characters
const INIT: TravelState = TravelState {
hours: 0,
fails: 0,
damage: 0,
};
}
I decided to export a states vector where the index in the vector matched the transition matrix index. In this way, the matrix could have as small as a rank as possible. Thus, build_transition_matrix returns both a transition matrix and a states vector for interpreting the states.
/// Return a vector of travel states and a Markov transition matrix, representing a character
/// travelling through the blizzard to Karlensburg. The sparse matrix values are transition
/// probabilities, represented as float in the range 0 to 1.0 (although zeroes are not stored
/// explicitly in the matrix). The indices of the travel states correspond to the row and column
/// indices of the transition matrix.
///
/// Every state leads to two additional states until the character has finished the journey, after
/// either seven or ten transitions, in which case the states transition to themselves. For a seven
/// hour journey, there will be strictly less than 1 + 2 + 4 + ... + 128 = 255 states. For ten
/// hours, 1023.
fn build_transition_matrix(
character: &Character,
hours: u8,
) -> (Vec<TravelState>, sprs::CsMatI<f32, usize>) {
// Since multiple transitions may lead to the same state, prev_states/next_states is a set
// rather than a list so we avoid duplicates.
let mut prev_states: BTreeSet<TravelState> = BTreeSet::new();
prev_states.insert(TravelState::INIT);
let mut next_states: BTreeSet<TravelState> = BTreeSet::new();
let mut vertices: Vec<TravelState> = Vec::new();
vertices.push(TravelState::INIT);
let mut edges: Vec<(TravelState, TravelState)> = Vec::new();
for hour in 1..=hours {
for prev_state in &prev_states {
let success = TravelState {
hours: hour,
fails: prev_state.fails,
damage: prev_state.damage,
};
let fail = TravelState {
hours: hour,
fails: prev_state.fails + 1,
damage: prev_state.damage + hour,
};
vertices.push(success);
edges.push((*prev_state, success));
next_states.insert(success);
vertices.push(fail);
edges.push((*prev_state, fail));
next_states.insert(fail);
}
mem::swap(&mut prev_states, &mut next_states);
next_states.clear();
}
// for the final hour, the states should transition to themselves
for prev_state in &prev_states {
edges.push((*prev_state, *prev_state));
}
prev_states.clear();
vertices.sort();
vertices.dedup();
let mut mat = sprs::TriMatBase::with_capacity((vertices.len(), vertices.len()), edges.len());
for (src, dst) in edges {
mat.add_triplet(
vertices.binary_search(&dst).unwrap(),
vertices.binary_search(&src).unwrap(),
character.prob(src, dst),
);
}
(vertices, mat.to_csr())
}
Using a breadth-first approach, I generate states (vertices within the graph) for each hour traveled. I also generate the edges, although the edges aren’t labeled with probabilities yet. Terminal states in the transition matrix must be represented as transitioning to themselves, so I have to include some special handling of that case. Finally, we build the sparse matrix by looping through the edge list and calculating the probability of traversal. The probabilities are stored as f32 or 32-bit floats. Given the small range, I thought of using f8 or one of the reduced bit formats, but since we are using sparse matrices and we do not need to worry about running in memory constrained browsers, it would be a trivial optimization.
The actual computation of the probability is handled within survival. The initial state vector has a 1 in the first index (corresponding to the initial state being stored first in the vector), representing that, absent a transition, there is a 100% chance of being in the initial state. Then, we perform the multiplications and sum the results based on whether a particular travel state would indicate that the character survived or not.
/// Compute the survival probability (probability of surviving alive, probability of dying in the
/// blizzard) for a character travelling the specified number of hours. The `states` and `transition`
/// arguments should be the output of the `build_transition_matrix` function.
fn survival(
hours: u8,
character: Character,
states: Vec<TravelState>,
transition: sprs::CsMatI<f32, usize>,
) -> (f32, f32) {
let initial = sprs::CsVec::new(states.len(), vec![1], vec![1.0f32]);
// Within a Markov chain, the probability after n transitions of a transition matrix A
// is equal to A**n * x, where x is in the initial state column vector.
let mut m = transition;
for _ in 0..hours {
m = &m * &m;
}
m = &m * &initial.col_view();
// Why treat the two probabilities as independent? This is a way to verify the process has
// resulted in values where p and not p is equal to 1 (or sufficiently close).
let mut alive_prob = 0.0;
let mut dead_prob = 0.0;
for (prob, (row, _)) in m.iter() {
if character.is_dead(states[row]) {
dead_prob += prob;
} else {
alive_prob += prob;
}
}
(alive_prob, dead_prob)
}
The Odds
Assuming each character has taken no prior damage (not a sure thing in this adventure), the probability of successfully making the trip to Karlensburg is:
| Character Name | CON | HP | P(success) | 7 hr | P(success) | 10 hr |
|---|---|---|---|---|
| Anton Berrudzeck | 14 | 15 | 59 | 16 |
| Boris Sturkl | 15 | 15 | 67 | 24 |
| Hans Winklemann | 13 | 11 | 33 | 8 |
| Johann | 18 | 18 | 93 | 68 |
| Belinda Chadaver | 14 | 12 | 46 | 13 |
| Beatrice Chadaver | 16 | 16 | 78 | 36 |
| Phillipe d’Isigny | 11 | 12 | 23 | 3 |
| Yurik Drozopczech | 14 | 14 | 56 | 15 |
As you can see, the seven hour trip is treacherous but survivable for a few characters. The ten hour trip is dangerous even for Johann. The probability of the entire party making the journey successfully is a mere 0.5% and the ten hour trip 0.00004%.
If we plot the survivability matrix for all CON scores 3 to 18 and hit points of 1 to 20 (below; csv), we can see that the probabilities are pretty grim, particularly if characters have taken damage before.
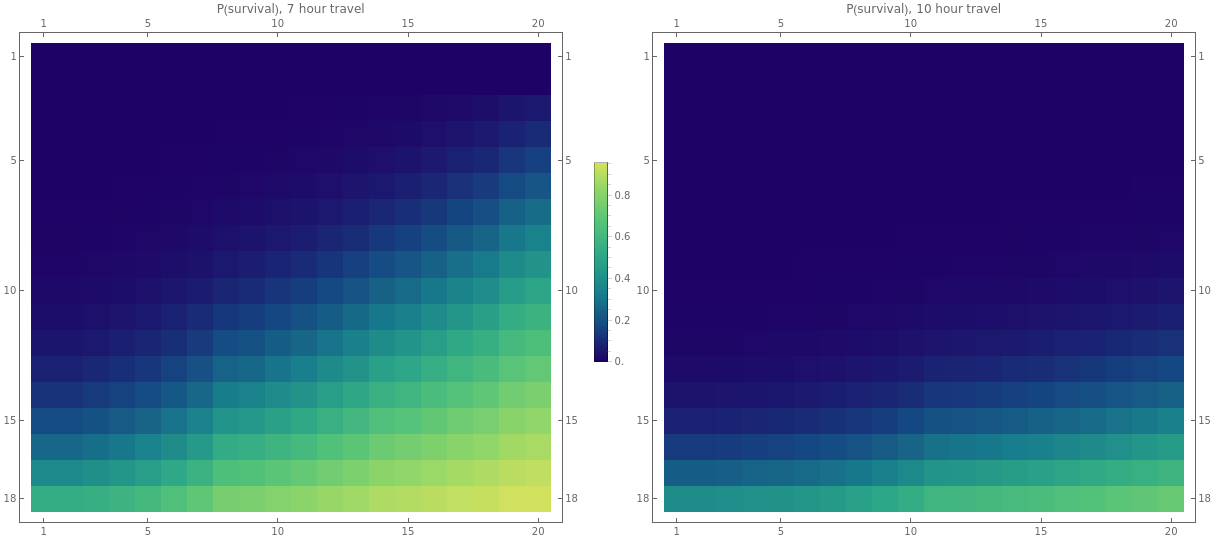
Of course, the alternative may provide even less of a chance of survival…
References
[1] Love, Penelope. “Chateau of Blood.” Blood Brothers 2, edited by Lynn Willis, Chaosium Inc., 1992, 23-37.
[2] Ibe, Oliver C.“Introduction to Markov Processes.” Markov Processes for Stochastic Modeling, Elsevier Academic Press, 2009, 45-46.
[3] Ibe, Oliver C.“Discrete-Time Markov Chains.” Markov Processes for Stochastic Modeling, Elsevier Academic Press, 2009, 55-58.